TEORI GRAPH, SEJARAH DAN MANFAATNYA
Graph sering digunakan untuk merepreesntasikan sebuah objek dan hubungannya dengan objek lain. Sejarah teori graph bermula saat ahli matematika Swiss Leonhard Euler memecahkan masalah jembatan Königsberg . Masalah jembatan Königsberg adalah teka-teki lama mengenai kemungkinan menemukan jalan setapak di tujuh jembatan yang membentang di sepanjang sebuah sungai bercabang yang melewati sebuah pulau tapi dengan tanpa melewati jembatan dua kali. Euler berpendapat bahwa tidak ada jalan semacam itu. Buktinya hanya mengacu pada susunan fisik jembatan, namun intinya dia membuktikan teorema pertama dalam teori graph (Carlson, 2017).
Seperti yang digunakan dalam teori grafik, grafik istilah tidak mengacu pada grafik data, seperti grafik garis atau grafik batang. Sebaliknya, ini mengacu pada sekumpulan simpul (yaitu titik atau simpul) dan tepi (atau garis) yang menghubungkan simpul. Bila dua simpul digabungkan lebih dari satu tepi, grafiknya disebut multi graph. Grafik tanpa loop dan paling banyak satu tepi antara dua simpul disebut grafik sederhana. Kecuali dinyatakan lain, grafik diasumsikan mengacu pada grafik sederhana. Bila setiap simpul dihubungkan oleh ujung ke setiap titik lainnya, grafik disebut grafik lengkap. Bila sesuai, arah dapat diberikan ke masing-masing ujung untuk menghasilkan apa yang dikenal sebagai grafik terarah, atau digraf (Carlson, 2017).
Graph pada dasarnya mempunyai komponen berupa simpul dan sisi dan pada graph tersebut sehingga membentuk graph terbuka dan graph tertutup sehingga membentuk sejumlah lintasan dan sirkuit. Sehingga pada teorema graph telah dapat menyelesaikan tanda tanya dalam penyelesaian teka-teki jembatan Konigsberg dan dengan solusi masalah yang sama (Wirdasari, 2011).
- Masalah di Konigsberg (7 crossing point on progel river)
Euler adalah seorang ahli matematika yang mencoba untuk memecahkan teka-teki tersebut dan lebih dikenal dengan masalah Jembatan Konigsberg (Wirdasari, 2011). Terdapat 7 (tujuh) buah jembatan yang dapat menghubungkan 2 (dua) pulau dan juga sebuah sungai, seperti yang ditunjukkan pada Gambar 1 .
Gambar 1. Jembatan Konigsberg (Wirdasari, 2011)
- Urban planning problem
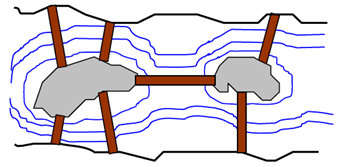
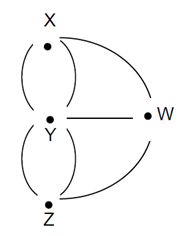
Dalam mecari solusi tersebut euler seorang matematika tersebut mencoba metode dari masalah ini adalah dengan membentuk model dari jembatan Konigsberg yang dikenal dengan multigraph, diperlihatkan pada Gambar 2. Pada multigraph tersebut memiliki 2 (dua) elemen yaitu himpunan verteks (titik/node) dan himpunan edge (garis) yang saling menghubungkan garis antar verteks (Wirdasari, 2011).
Gambar 2. Representasi Multigraph Jembatan Konigsberg (Wirdasari, 2011)
Titik-titik yang diberi label X, Y, Z, dan W pada Gambar 2 itulah yang disebut verteks dan dengan garis saling menghubungkan antar titik itulah yang disebut dengan edge.
Pada semua multigraph euler telah membuat sebuah aturan yang dapat dipakai dalam mencari solusi pada jembatan Konigsberg, sehingga aturan ini disebut dengan sebutan Eulerian path, yang berbunyi:
“Andai kita mempunyai sebuah multigraph untuk beberapa pasang verteks sehingga akan terdapat sebuah path (lintasan) diantara verteks-verteks tersebut. Multigraph tersebut memiliki eulerian path dan jika terdapat 0 datau 2 verteks tersebut maka banyak edge yang meninggalkan verteks tersebut akan berjumlah ganjil”
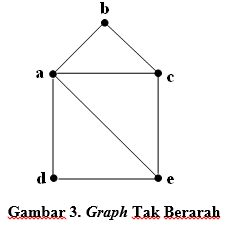
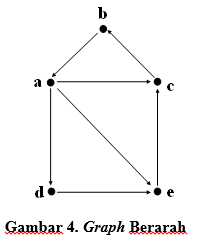
Pada Multigraph jembatan Konigsberg tersebut memiliki empat verteks dan pada ke-empat verteks tersebut memiliki edge sehingga meninggalkan verteks yang berjumlah ganjil. Maka Eulirian path tersebut tidak dimiliki pada multigraph jembatan Konigsberg. Multigraph yang ditunjukkan pada Gambar 3 tidak memiliki panah, sehingga disebut dengan undirected graph (graph tak berarah). Sehingga disebut dengan directed graph (graph berarah) adalah multigraph yang memiliki panah yang ditujukan pada gambar 4.
Definisi 1. Sebuah simple graph (undirected graph) adalah pasangan dari G = (V , E) dimana:
- V = himpunan berhingga dari elemen yang disebut verteks
- E = sebuah relasi yang irrefleksif dan simetri pada V.
Pasangan berurutan pada E disebut edge dari graph yang berurutan . Lebih spesifik, jika e = (u, v) Î E , dikatakan bahwa edge e adalah antara u dan v (dan juga antara v dan u ), dan dikatakan bahwa u adjacent ke v . Lebih jauh, dapat dikatakan bahwa e incident ke u (dan juga v ). Karena E simetri, maka kita dapat menotasikan e sebagai pasangan tak berurut {u, v}.
- Pemecahan oleh Euler
Hasil dari Teka-Teki Jembatan Konigsberg berdampak sungguh luar biasa terhadap ilmu pengetahuan. Dari teka-teki tersebut sangat berguna dan telah membuka jalan bagi terciptanya teorema baru yang disebut teorema graph. (Studi & Informatika, n.d.).
Pada Teka-Teki Tujuh Jembatan Konigsberg menghasilkan solusi permasalahan dengan dapat diperolehnya melalui dianalogikannya setiap jembatan sebagai sisi dan setiap daratan yang diperolah sebagai simpul pada graph sehingga dapat terbentuknya graph yang lengkap. Dengan memperhitungkan derajat dalam graph dari setiap simpulnya maka dengan menggunakan metode seperti yang telah diungkapkan dalam pembuktian di atas, kita akan dapat mengetahui apakah graph tersebut merupakan suatu lintasan di mana setiap sisi dilalui hanya satu kali saja (Studi & Informatika, n.d.).
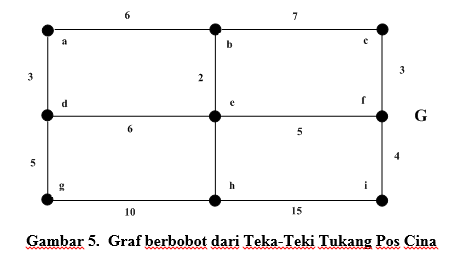
Fakta bahwa teorema graph yang dihasilkan oleh Euler telah menyelesaikan masalah berdasarkan Teka-Teki pada Jembatan Konigsberg yang menyatakan hubungan tersendiri antara jaringan spasial (seperti jalur transportasi) pada graph. Dalam memodelkan jaringan spasial, sebagai ada beberapa tambahan yaitu selain simpul dan sisi adalah biasanya diberikan sebuah nilai selaku bobot berupa panjang atau satuan ukuran nilai lainnya yang menyatakan kuantitas segmen jalan yang diwakili oleh sisi pada graph tersebut. Maka selanjutnya kita dapat mencari suatu rute pada jaringan spasial tersebut yaitu menggunakan sarana atau beban yang minimal seperti pada solusi Teka-Teki Tukang Pos Cina (Studi & Informatika, n.d.).
Gambar 6. Berat minimum matching sempurna dari graf lengkap K
manfaat dari mempelajari salah satu aplikasi Teorema Euler, dapat diketahui dari hasil kerja Euler mengenai graph merupakan menjadi salah satu kunci penting dalam keberhasilan penyelesaian berbagai aplikasi masalah yang ada di dunia nyata.
- Teknologi Graph Database
Dalam komputasi, database graf adalah database yang menggunakan struktur grafik untuk query semantik dengan node, edge dan properti untuk mewakili dan menyimpan data. Konsep kunci dari sistem adalah grafik (atau edge atau hubungan), yang secara langsung menghubungkan item data di toko. Hubungan memungkinkan data di toko dihubungkan secara langsung, dan dalam banyak kasus diambil dengan satu operasi.
Mengambil data dari database grafik memerlukan bahasa query selain SQL, yang dirancang untuk manipulasi data dalam sistem relasional dan oleh karena itu tidak dapat “secara elegan” menangani pelacakan grafik. Pada tahun 2017, tidak ada bahasa query grafik tunggal yang telah diadopsi secara universal dengan cara yang sama seperti SQL untuk basis data relasional, dan ada beragam sistem, yang paling sering terkait erat dengan satu produk. Beberapa upaya standardisasi telah terjadi, yang mengarah ke bahasa query multi-vendor seperti Gremlin, SPARQL, dan Cypher. Selain memiliki antarmuka bahasa query, beberapa database grafik diakses melalui antarmuka pemrograman aplikasi (API).
Grafik database didasarkan pada teori grafik, dan menggunakan node, edge, dan properti.
- Node mewakili entitas seperti orang, bisnis, akun, atau item lainnya untuk dilacak. Mereka kira-kira setara dengan catatan, relasi, atau baris dalam database relasional, atau dokumen dalam database dokumen.
- Edge, juga disebut grafik atau hubungan, adalah garis yang menghubungkan node ke node lain; mereka mewakili hubungan di antara mereka. Pola bermunculan muncul saat memeriksa koneksi dan interkoneksi node, properti, dan edge. Edge adalah konsep kunci dalam database grafik, mewakili abstraksi yang tidak langsung diimplementasikan di sistem lain.
- Properti adalah informasi yang sangat bagus untuk node. Misalnya, jika Wikipedia adalah salah satu simpul, mungkin terkait dengan properti seperti situs web, materi referensi, atau kata-kata yang dimulai dengan huruf w, bergantung pada aspek Wikipedia mana yang sesuai dengan database tertentu.
By : Dimas Aji Pamungkas , Eduard Pangestu Wonohardjo, Rizky Febriyanto Sunaryo, Yusuf Sudiyono
Daftar Pustaka :
Carlson, S. C. (2017). Graph theory. Retrieved from https://www.britannica.com/topic/graph-theory
Studi, P., & Informatika, T. (n.d.). Jembatan konigsberg, 1–10.
Wirdasari, D. (2011). Teori graph dan implementasinya dalam ilmu komputer, 10(1), 23–34.
https://en.wikipedia.org/wiki/Graph_database