Criptography: Authetication Zero knowledge proof
Yonathan Marcellinus dan Benfano Soewito
Zero knowledge proof pertama kali dikenalkan dan dipublikasikan oleh (Jacques, Guilou, & Berson, 1990) pada paper yang berjudul “How to Explain Zero-Knowledge Protocols to Your Children”. Zero knowledge proof adalah konsep yang sangat populer dan banyak digunakan dalam sistem kriptografi. Dalam konsep ini, ada dua pihak yang terlibat yaitu prover dan verifier. Dengan teknik ini memungkinkan seorang prover menunjukkan bahwa dia memiliki hak atau bukti ( credential ) tanpa harus menunjukkan nilai yang sebenarnya kepada verifier. Zero knowledge proof banyak digunakan untuk sistem otentikasi karena memiliki sifat – sifat sebagai berikut :
- Completeness : Jika pernyataan tersebut memang benar, maka verifier akan dapat membuktikan pernyataan itu benar secara berulang-ulang.
- Soundness : Jika pernyataan itu salah, tidak akan ada kecurangan yang dapat dilakukan prover untuk dapat meyakinkan verifier bahwa pernyataan tersebut benar. Kecuali dengan beberapa kemungkinan kecil.
- Zero-knowledge : Jika pernyataan itu benar, tidak akan ada pengetahuan apapun yang didapatkan selain fakta tersebut. Hal ini ditunjukkan dengan sebuah simulasi yang menunjukkan bahwa pernyataan itu benar dan tidak ada yang diperoleh verifier dari prover.
Jean Jacques Q dan Louis Guillou mengilustrasikan zero-knowledge proof dengan menggunakan sebuah cerita tentang goa yang memiliki rahasia. Dalam ilustrasi ini dikenal dua orang tokoh Peggy ( prover ) dan Victor ( verifier ).
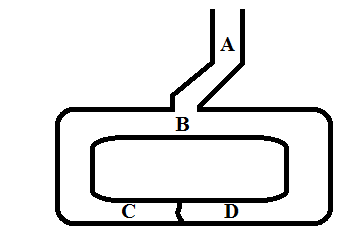
Gambar 1 – Ilustrasi Zero knowledge proof
Seseorang yang mengetahui kata kunci dapat membuka pintu rahasia antara C dan D. Misalkan Peggy ingin membuktikan kepada Victor bahwa dia mengetahui kata kunci untuk membuka pintu rahasia, maka yang perlu Peggy dan Victor lakukan adalah sebagai berikut:
- Victor berdiri di titik A
- Peggy berjalan masuk kedalam gua menuju titik C atau D
- Setelah Peggy tidak terlihat di dalam gua, Victor berjalan ke titik B
- Victor kemudian memerintahkan kepada Peggy untuk :
- Keluar dari jalur sebelah kiri atau sebelah kanan
- Peggy kemudian akan merespon, dan menggunakan kata kunci yang ia miliki untuk membuka pintu rahasia, jika seandainya ia benar-benar punya.
- Peggy dan Victor kemudian akan mengulangi langkah – langkah tersebut sampai n kali.
Dengan metode ini, Victor tidak akan mungkin meyakinkan pihak ketiga tentang bukti kepemilikan rahasia oleh Peggy dan dia juga tidak dapat memperoleh informasi apapun tentang informasi rahasian yang diketahui oleh Peggy. Hal ini mengakibatkan tidak mungkin Peggy dapat menebak secara tepat secara terus menerus sisi sebelah mana Victor akan meminta keluar. Probabilitas Peggy dapat menebak dengan secara tepat seperti ini akan sangat kecil apabila dilakukan secara berulang-ulang (Schneier, 1996).
2.1. Zero Knowledge Proof of Knowledge Discrete Logarithms
Dalam penerapan Zero Knowledge Proof dilakukan dengan perhitungan matematika, salah satunya dengan perhitungan Discrete Logarithms. Pada paper “Implementing Zero-Knowledge Authentication with Zero Knowledge (ZKA•wzk)” (Brandon, 2010) membahas teknik tersebut yang digunakan untuk authentication web dengan perhitungan Discrete Logarithms. Algoritma ini berlandaskan dari (Camenisch, 1998) Zero Knowledge Proof of Knowledge Sigma Protocol menggunakan SPK1 {(x) : Y = g0x}. Dengan proses – proses sebagai berikut :
- Inisialisasi :
- Diketahui sebuah Group G dan g0, g1 didapatkan dari random element dari G.
- Maka G dan g0 menjadi public key.
- Registrasi :
- User memasukkan username dan password.
- Kemudian password di hashing dengan fungsi hash. diperoleh x = hashing ( password ).
- User melakukan perhitungan untuk Y = g0x.
- Kemudian user mengirim (username,Y) ke server.
- Server menyimpan username,Y.
- Authentication Process :
- Server melakukan generate random variabel a, menyimpannya dan mengirimkannya ke client.
- User memasukkan username dan password.
- Client melakukan hash ke password dengan fungsi hash, dan menghitung x = hash(password).
- Client menghitung Y = g0x.
- Client melakukan generate random rx € G dan hitung T1 = g0rx.
- Client menghitung c=hash(Y,T1, a) dan zx= rx-cx.
- Client mengirim (c, zx) ke Server.
- Server menghitung T1 = Yc g0zx dan mencocokkan c = hash(Y, T1, a)
- Jika sesuai, maka User telah di otentikasi.
Teknik ini merupakan teknik umum yang digunakan untuk membuktikan pengetahuan tentang variable yang berkaitan dengan password. Berikut penjelasan untuk setiap komponen yang digunakan dalam algoritma ini :
Tabel 1 – Penjelasan komponen Zero Knowledge Authentication
| Component | Description |
| G | Merupakan serangkaian angka yang berdasarkan pada formula. Kumpulan angka ini bersifat public dan dapat diakses oleh kedua pihak , Client ( Prover ) dan Server ( Verifier ). |
| g0 | Sebuah angka yang diperoleh dari G dan merupakan elemen dari G. Variabel ini bersifat public dan dapat diakses oleh kedua pihak ( prover dan verifier ). |
| x | Hasil hash dari password yang di-input oleh prover. |
| Y | Sebuah alias password dari prover. Digunakan verifier untuk menghitung proof of knowledge. |
| a | Random token yang di-generate setiap prover melakukan login. |
| T1,rx,zx,c | Variabel lainnya yang digunakan dalam kalkulasi. |
| Legend :
Nilai Public – Diketahui oleh prover dan verifier. Nilai rahasia server – Tetapi dapat diturunkan kepada prover ( client ). Nilai rahasia client – Hanya diketahui oleh prover ( client ). |
|
Dengan pengetahuan tersebut, maka algoritma dapat bekerja. Untuk menjalankan algoritma itu maka G harus di-generate dari sebuah angka seperti {1,2,3,4,..}, dan g0 didapatkan dari hasil random angka dalam G. Algoritma itu menggunakan g0 yang berasal dari G sehingga sulit mendapatkan perhitungan logaritma diskrit.
Table 2 – Nilai yang dimiliki pada proses authentication
| Prover ( User ) | Verifier ( Server ) |
| g0 | g0 |
| Password | Y |
Tabel 3 – Proses authentication
Dari formula perhitungan yang dilakukan, diketahui T1 dihitung tanpa mengetahui pengetahuan apapun karena rx diperoleh dari hasil random. Diperoleh persamaan sebagai berikut :
- Langkah 8 : T1 = g0rx
- Langkah 13 : T1 =Yc g0zx
- Maka diperoleh persamaan : g0rx = Yc g0zx
- Langkah 5 : Y = g0x
- Langkah 11 : zx = rx – cx
- Lakukan subtitusi :
g0rx = Yc g0zx
g0rx = ( g0x )c g0(rx-cx)
g0rx = g0cx g0rx-cx
g0rx = g0cx+rx-cx
g0rx = g0rx ( Diterima )
Dari persamaan tersebut diketahui, dengan ketiga elemen tersebut maka dapat dibuktikan bahwa c = hash(Y, T1, a) dan user mengetahui nilai x.



Comments :