Generative Additve Model (GAM)

GAM merupakan model pengembangan adaptasi General Linear Model (GLM) yang pertama kali dikembangkan sejak tahun 1986. Dalam pengembanggannya GAM memiliki fleksibilitas lebih tinggi, karena hubungan variabel predictor yang ditangkap smoother function tidak berasumsi harus linear.

Konsep smoother dalam interpretasi model prediksi ditunjukkan pada gambar 1 dengan menggabungkan fungsi model berdasarkan masing-masing ciri khas pola variabel predictor terhadap waktu. Sehingga dapat ditarik kesimpulan, berdasarkan konsep additive rumus GAM dalam persamaan 1 sebagai berikut:

Dari persamaan 1, Y melambangkan variabel dependent atau parameter yang ingin diprediksi, E(Y) melambangkan expected value, g(Y) menggambarkan fungsi gabungan yang diharapkan pada variabel predictor x. Serta elemen s(x) berperan sebagai smooth function atas setiap variabel predictor x yang bersifat nonparametric.

Terdapat beberapa alasan menarik mengapa GAM sering digunakan sebagai model prediksi time series, yaitu:

1. Interpretability

Dengan model akhir, kita dapat menganalisis kecenderungan pergerakan garis model berdasarkan variabel predictor. Sebagai contoh, tren s_p(x_p) meningkat seiring dengan meningkat secara linear variabel x_p. Dan keunggulan berikutnya adalah pengaturan smoother agar menghindari hasil prediksi yang dirasa aneh. Karena pada kasus nyata, banyak gangguan dalam dataset yang mempengaruhi.

2. Flexibility

Proses fitting model kadang membutuhkan waktu yang cukup lama untuk dapat mencari model terbaik yang dapat menangkap pola nonlinear dengan baik. Namun, GAM secara otomatis dapat menangkap pola nonlinear yang terlewat oleh metode linear untuk menentukan predictor function terbaik saat menentukan model. Dengan kemampuan ini, peneliti dapat menghemat waktu dan mendapatkan informasi function yang benar-benar dibutuhkan.

3. Regularization

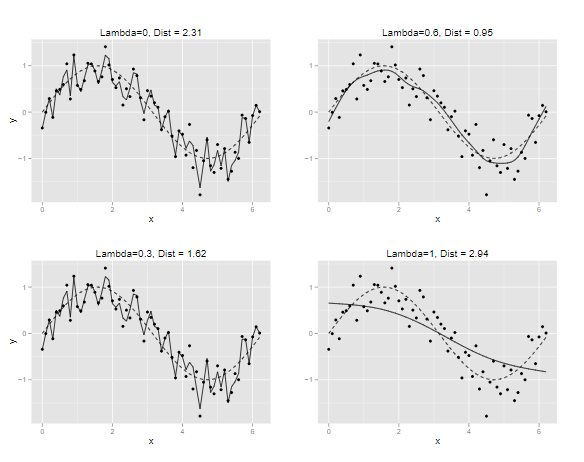
Berhubungan dengan kebebasan untuk mengatur smoother function yang telah dijelaskan sebelumnya, GAM dapat mencegah overfitting. Pengaplikasian bayesian regression dan L2 regularization dapat menangani bias pada predictor function. Dengan catatan penting semakin besar nilai λ smooth function maka model akan lebih halus. Sebagai perbandingan apabila nilai λ=0, model akan menyesuaikan data dengan baik. Namun lengkungan garis pada model akan terlihat kaku sehingga kurang dapat menggambarkan hubungan yang sesuai antara predictor dengan dependent variable. Dan apabila nilai λ=1 maka kurva model akan tampak lebih halus, namun terdapat juga kemungkinan besar untuk gagal menangkap pola penting hubungan antar data. Untuk penggambaran lebih lanjut dapat dilihat pada gambar 2, terdapat perbedaan pergerakan kurva dengan nilai nilai λ yang berbeda.

Gambar 2 Pengaruh smoother (λ) dalam GAM

Disadur dari :

Fernando Lioexander, Abba Suganda Girsang, Arsitektur Prophet Dalam Prediksi Normalisasi Meteran Konsumsi Energi Pada Bangunan,  Tesis, Universitas Bina Nusantara, Jakarta. 2021